In this study, a simple numerical tool was developed and implemented to address actual management issues related to the positioning of oyster Crassostrea virginica farms in the Richibucto Estuary (eastern Canada). The versatile procedure relied on hydrodynamic modelling and tracer advection−dispersion to reproduce the spatial and temporal dynamics of seston availability. The model identified 3 areas of interest within the estuary, each with unique water renewal rates and seston concentrations. The method also revealed major interactions between the different areas, and proved efficient in quantifying the effects of topographical alterations on seston availability. Our results suggest that such basic modelling tools produce relevant information in a timely manner, and thereby facilitate the necessary dialogue between science advisors, industry stakeholders and resource managers.
Introduction
One of the major limitations to the development of shellfish aquaculture in coastal areas is the intraspecific competition among the cultured individuals. The ability of these organisms to clear large volumes of water of their organic particle contents may lead to an overall reduction in food availability, which translates into a limited production capacity.
Matching the shellfish stocks with naturally available organic seston, i.e. bivalve food (henceforth seston), is a recurrent challenge shellfish growers are facing and has been a prime research question for decades. Studies have addressed this food shortage issue at different scales, from the boundary layer over a mussel bed (Fréchette & Bourget 1985, Smaal & Haas 1997) to the raft or farm scale (Incze et al. 1981, Aure et al. 2007, Rosland et al. 2011) and up to the bay, estuary or lagoon scale (Bacher et al. 1997, 2003, Dame & Prins 1997, Duarte et al. 2003, Grant et al. 2008, Filgueira & Grant 2009, Cugier et al. 2010, Guyondet et al. 2010). Most of these contributions were based on a combination of field data collection and different mathematical frameworks, scaling and comparing seston demand and supply at the chosen physical extent.
Despite the amount of literature gathered in this field and the numerous modelling strategies developed, tools specifically designed for industry and management stakeholders that aim at informing the farm site selection process as well as the development of the shellfish culture activity are still needed (Silva et al. 2011). The seston availability issue usually amounts to the comparison of 3 basic processes: physical water renewal, planktonic primary production and bivalve biomass filtration. Their variability and interactions force the use of complex tools not suitable for non-experts. One of the few exceptions is the so-called Dame Index (Dame & Prins 1997), which compares static estimates of the time scales of the 3 aforementioned processes for a given coastal system (primary production time, PPT; bivalve clearance time, CT; and water renewal time, RT, evaluated with the tidal prism method; Dyer 1973). Although misleading at times (Guyondet et al. 2005), this index is still supported for estimating potential effects of cultured shellfish on planktonic resources (ASC 2012).
Dowd (2003) proposed a minimal framework to carry out a dynamic comparison of the 3 processes at work. The simple numerical method is based on hydrodynamic modelling and advection–dispersion of a tracer simulating the transport, production and consumption of seston. Despite its relative ease of implementation, the method has not been applied to different actual scenarios or to address management issues.
Following a rapid development phase since the 1980s, the shellfish aquaculture industry in Atlantic Canada is presently entering a management phase. In this context, the demand for scientifically-based tools for estimating carrying capacity will inevitably increase. This is certainly the case for the Baie du Village, an embayment within the Richibucto Estuary in the province of New Brunswick, where a moratorium on new aquaculture development has been imposed since 2007. The reassessment of the latter, in 2012, emphasized the need for an evaluation of the present level of development with respect to planktonic resource utilization. A previous study in Richibucto Estuary, focused on a distinct area (Koutitonsky et al. 2004), nevertheless advised monitoring the evolution of a breach in the main sand barrier, as it had the potential to substantially modify water circulation in the Baie du Village area.
The main objectives of the present work were to (1) demonstrate the advantages of the method developed by Dowd (2003) through its application to a real case study involving various management issues; and (2) test more specifically for the breach effect on hydrodynamics and seston availability.
Materials and Methods
Study area—2010 sampling
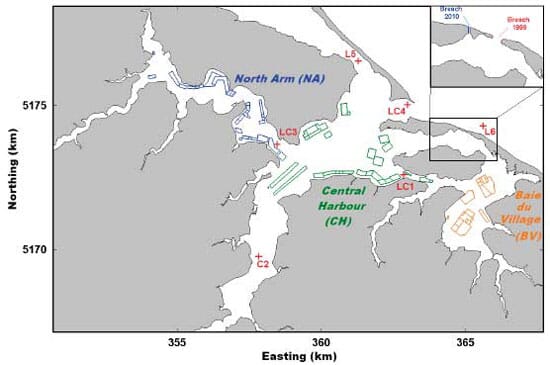
The Richibucto Estuary is located in southeastern New Brunswick along the Northumberland Strait (Fig. 1). It is a semi-enclosed bar-built estuary typical of many coastal embayments in Atlantic Canada. It comprises 3 main areas (see Fig. 2). The open Central Harbour (CH) connects the Richibucto River upstream with the Gulf of Saint Lawrence through the main navigation channel (width 150 m and depth 8 to 10 m). The North Arm (NA) is characterized by a narrow channel (depth 2 to 4 m) leading to the St Charles River. Finally, Baie du Village (BV) is a shallow em - bayment (2 to 3 m) linked to the harbour through 2 narrow passes north and south of Indian Island. The sand dune to the south of the main inlet presents a narrow breach (width 25 to 30 m and depth 1.2 m) that has been moving west and filling up since the last re - ported observations in 1999, at which time it was 200 m wide and 1.5 to 2.0 m deep (Koutitonsky et al. 2004).
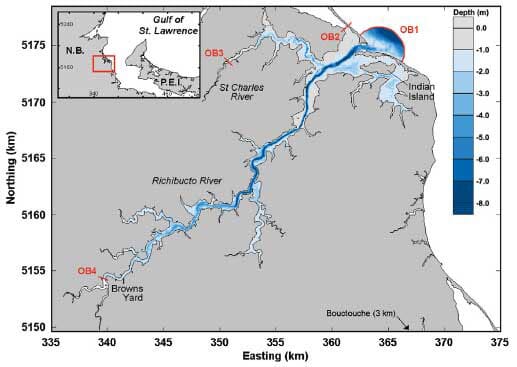
In order to force and calibrate a hydrodynamic model of the estuary, tide gauges (Water Level Data Logger HOBO, Onset Computer Corporation) and current meters (Sontek Argonaut-XR, YSI/Xylem and Workhorse Sentinel, Teledyne RD Instruments) were moored at locations shown in Fig. 2 during the summer of 2010 (25 June to 5 August). Meteorological data (wind speed, direction and atmospheric pressure) were retrieved from the Environment Canada station in Bouctouche, 25 km south of the study area. Daily freshwater discharges of the St Charles (0.2 to 2.0 m3 s−1) and Richibucto (1 to 9 m3 s−1) rivers were calculated from observations made at Environment Canada station 01BS001 located upstream of Browns Yard (Fig. 1). Discharges recorded at the Environment Canada station were scaled to the corresponding watershed areas of 226 and 1100 km2 for the St Charles River and Richibucto River, respectively.
Numerical model
The present modelling work was carried out using the RMA10-RMA11 suite of finite element models (King 1982, 2003). RMA10 is the hydrodynamic engine that solves the Reynolds form of the Navier-Stokes equations for momentum, the continuity equation and a convection−diffusion equation for transport of heat, salinity and any dissolved or suspended matter. It uses a Smagorinsky scheme (Smagorinsky 1963) to estimate horizontal eddy diffusivities. RMA11 is a biochemical module that allows specifying the properties of any substance transported according to the convection−diffusion equation.
Application to the Richibucto Estuary
The following numerical experiments were conducted using a 2-dimensional, vertically averaged representation of the estuarine system that was thought to capture the main features of the hydro - dynamics during the low freshwater run-off period.
Calibration
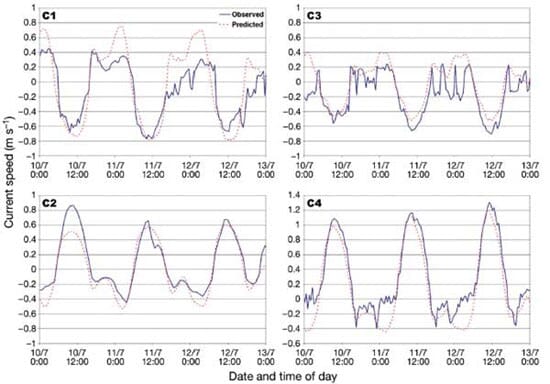
The 2010 data set was used for hydrodynamics calibration purposes. The model presents 4 open boundaries (Fig. 1) that were forced by observed water levels (OB1 and OB2 forced by observations at stations L6 and L5, respectively) or freshwater discharges (OB3 and OB4) determined as mentioned in the previous section. For this procedure, the model was also forced by wind stress at the free surface to complete a natural set of forcing. The only parameter of the hydrodynamic model to be calibrated was the bottom friction scaled by a unique Manning coefficient (n) over the whole domain. The calibration was achieved by comparing model predictions with observed water levels and current time series at inner stations (LC1, C2, LC3 and LC4) over the period 25 June to 5 August. A brief overview of these calibration results is included in 'Results and Discussion'.
Working simulations
For the remainder of the study, longer simulations were required. Hence, observed water levels were replaced by tidal predictions obtained by the harmonic analysis of observed series (Foreman 1977), and surface forcing was removed. The model reproduced the system dynamics under the influence of tides and freshwater discharge over a 120 d period extending from 20 June to 18 October. The model was run for 2 configurations: 2010 and 1999 that only differed by the morphology of the breach in the sand dune (Fig. 2). The tidal forcing described above was used in both cases, as this exercise was meant to detect the effect of the change in morphology on the hydrodynamics of the estuary. Validity of the 1999 model results (not shown) was tested against a set of observations collected at that time (Koutitonsky et al. 2004).
Water renewal time
The contribution of water circulation to the dynamics of seston may be best illustrated by the spatial distribution of water renewal time, i.e. the time taken for water at any place in the estuary to be renewed by water from the outside (in the present case either freshwater or water from the Gulf of St Lawrence). The dissolved tracer method (Aubrey et al. 1993, Koutitonsky et al. 2004) was used to derive the water renewal time estimates. The convection−diffusion equation reproduces the spatio-temporal evolution of estuarine waters which are marked by a passive tracer (concentration C = 1 at time t = 0), as they are being renewed by the tracer-free waters (C = 0) of the rivers and Gulf of St Lawrence. Assuming an exponential decrease in concentration due to mixing, a location is considered as renewed when the tracer concentration falls below 1/e of the initial value. The time needed to reach this point is defined as the water renewal time (Aubrey et al. 1993, Ranasinghe & Pattiaratchi 1998).
Organic seston representation
The RMA11 module was used to define a suspended variable representing sestonic bivalve food. The dynamics of the seston are then reproduced by the convection−diffusion equation:
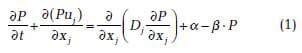
where P is the seston concentration in mg C m−3, uj is the current speed in direction xj calculated by the hydrodynamic model, Dj is the dispersion coefficient proportional to uj, α is the phytoplankton primary production rate in mg C m−3 d−1, and β is the bivalve population clearance rate in times per day.
The scaling factors linking Dj and uj are the only parameters that can be adjusted to tune the transport of dissolved and suspended matter reproduced by the model. Salinity data collected in August 2001 along a longitudinal transect extending from the mouth of the estuary to 35 km upstream in the Richi - bucto River (Koutitonsky et al. 2004) were used to check the validity of model results. For this purpose, a passive tracer representing salinity was set up with an initial uniform value of S = 25. The model was then forced with constant values of salinity corresponding to observations made at the upstream and downstream ends of the 2001 transect (S = 13 and S = 30, respectively). Results of this validation procedure are reported in 'Results and Discussion'.
The primary production rate α was estimated from in situ measurements made during the summer of 2011 in BV (L. A. Comeau unpubl. data) using the 14C method (JGOFS 1994). Its value was kept uniform over the model domain and constant during the simulation period and corresponded to a planktonic primary production rate of 75 g C m−2 yr−1. No previous report of primary production rates in the area could be found. However, the value used here falls well within observed rates for other estuaries of the region during the same 2011 campaign but sits at the lower end of the range (40 to 550 g C m−2 yr−1) reported for temperate estuaries (Heip et al. 1995).
The bivalve population clearance rate was calculated as the product of individual bivalve clearance rate (m3 ind.−1 d−1) and density of bivalves in the farm area (ind. m−2) and divided by depth. The clearance rate of the different size classes of oysters was de rived from Loosanoff (1958) and Powell et al. (1992). In Richibucto Estuary, oysters are grown either in floating bags or in floating cages with up to 6 bags cage−1 (Comeau et al. 2006). These husbandry practices result in a mean density of 904 bags ha−1 of farm, with each bag containing an average of 332 oysters (Comeau et al. 2006). The oyster clearance term (β ·P; Eq. 1) was only included in the model grid cells located inside the active farms (shown as polygons in Fig. 2).
Seston depletion index
In order to evaluate the net effect of transport, primary production and bivalve filtration on food availability, a seston depletion index (SDI) was calculated from the model results. The SDI is expressed as a percent change in seston concentration relative to the boundary concentration (P0) that was held constant during the simulations at a value P0 = 1000 mg C m−3, typical of summer seston concentrations in the area (Dowd 2003, Guyondet et al. 2005). To allow the seston concentration to reach an equilibrium state, we propose simulations for a period equal to or longer than the water renewal time of the area of interest. The concentration is then averaged over the last tidal cycle of the period at each node i of the model domain, and this averaged concentration Pavg is compared to the boundary value to estimate the SDI as follows:
The SDI is sensitive to seston depletion caused by bivalve filtration. SDI > 0 denotes a decrease in seston availability, whereas SDI < 0 reveals seston accumulation due to local primary production in less flushed areas. The SDI could be linked to Dame's approach (Dame & Prins 1997) by averaging its distribution over the whole system. At this global scale, SDI = 0 corresponds to the situation where bivalve filtration exactly matches the seston renewal by primary production, which is similar to PPT/CT = 1 in Dame's terminology.
Results and Discussion
Hydrodynamics
Model calibration
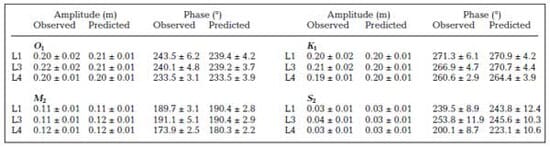
A Manning coefficient n = 0.015 led to the best fit between observations and model results. Comparisons of observed and predicted currents along their respective principal axis are presented in Fig. 3 for 2 full tidal cycles. These time series show a satisfactory agreement considering the variable nature of currents over short distances not captured by punctual measurements and the relatively coarse bathymetric information (nautical charts) that was available to build the model grid. Harmonic analysis was performed on both observed and predicted water level time series. Results for the main tidal constituents (Table 1) show that the model accurately reproduces the propagation of the tidal signal inside the estuary.
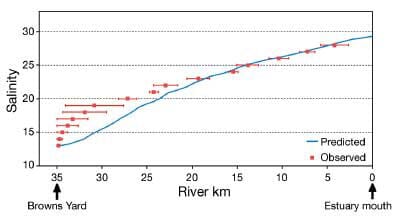
Salinity observations made in late August 2001 are thought to be representative of the distribution during low freshwater discharge, as Richibucto River discharges averaged 1.14 and 2.15 m3 s−1 during respectively 1 and 2 mo prior to the sampling date. This distribution may then be compared to the model results obtained with low freshwater discharges and averaged using the same procedure described above for the depletion calculation. Hence, factors scaling the diffusion coefficients to current velocity were tuned to reach the best agreement between observed and predicted longitudinal salinity distributions (Fig. 4). Model predictions agree very well with observations up to about 25 km upstream. The performance of the model decreases significantly in the upper reaches of the river. The horizontal bars in Fig. 4 show the longitudinal extent of a given salinity contour due to vertical stratification. From this and Fig. 4 in Koutitonsky et al. (2004), it is obvious that the upper portion of the river is characterized by a strong vertical stratification. The depth-averaged representation used in this study is not meant to reproduce the dynamics in such conditions, and the model is not expected to accurately describe mixing processes in this part of the system. However, the model results are reliable in the downstream section of the estuary, which is the main focus of this study.
Water renewal time
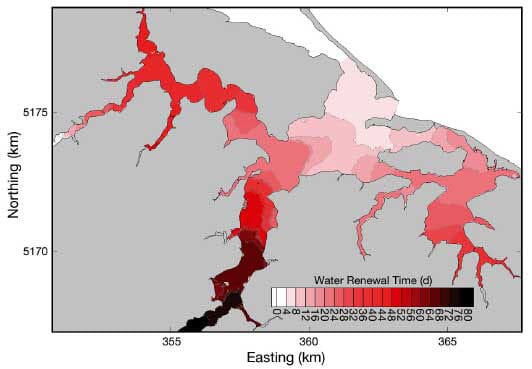
The spatial distribution of water renewal time within the studied area reveals 3 distinct regions (Fig. 5). CH is rather well flushed (5 to 20 d renewal time) due to the proximity of the inlet. On the eastern side, BV presents an intermediate level of flushing (18 to 35 d renewal time), since water has to travel part of the harbour and through the narrow passes around Indian Island before entering this embayment. Finally, the NA presents the longest renewal times (22 to 40 d renewal time) of all areas with aquaculture development. This result is mainly due to the distance from the inlet and the presence of the deeper channel that contributes to a rather high volume of water to be renewed. In addition, with low freshwater discharges during summer, the renewal effect of St Charles River is very limited. Koutitonsky et al. (2004) estimated a water renewal time of 20 d over most of the NA for low freshwater discharges. Al though the different frameworks (renewal of the NA alone in Koutitonsky et al. 2004, as opposed to renewal of the whole estuary in our study) prevent a direct comparison of the 2 estimates, the slightly longer renewal time obtained here is consistent with the Gulf of St Lawrence waters having to travel part of the CH prior to start renewing the NA.
Breach effect
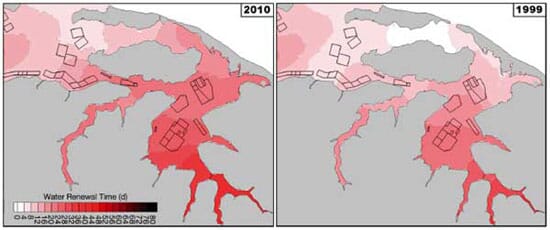
The water renewal time calculation was repeated for the model configured with the 1999 breach topo - graphy, but using identical forcing. The influence of the breach morphology can be seen in its immediate vicinity as well as in BV, which benefited from the improved exchange related to a wider, deeper and closer breach in 1999 than in 2010 (Fig. 6). The model suggests that aquaculture farms in BV were subjected to a 15 to 35 per cent decrease in water renewal since 1999.
Dynamics of organic seston
SDI results over the entire estuary are presented in Fig. 7. Again, 3 main regions may be distinguished. Due to its rapid water renewal, the CH barely presents any sign of seston depletion, except for the farms along the north shore. The very shallow waters of this area are subject to a strong filtering pressure, considering the small volume of water available per unit surface area. BV experienced stronger levels of de - pletion than NA (up to 29.5 and 8.7 per cent in BV and NA, respectively). The total farmed areas are very similar in BV and NA, but NA has a 24 per cent larger volume than BV, and the water renewal in NA is only 17 per cent slower than in BV on average. This may account for the stronger depletion predicted by the model in BV. Another source of discrepancy may come from the fraction of the renewing water already filtered by oysters from other parts of the estuary, which may differ between BV and NA. Additional information on this aspect is given below.
The SDI absolute values are not intended to represent an actual variation in seston concentration, as these estimates are subject to all model assumptions. It would also be extremely difficult to validate such a metric with field observations given the time and spatial scale involved in its variability (Grant et al. 2008, Strohmeier et al. 2008). Moreover, SDI estimates are not linked with oyster food requirements. Hence, depleted areas may not be interpreted as regions where food limitation would occur. The SDI must rather be seen as a relative criterion allowing the identification of potentially sensitive areas. It also allows a spatially detailed comparison of seston availability without tedious and expensive field sampling programmes.
Another methodological aspect needs consideration while interpreting these results. The decrease in seston concentration is expressed as depletion by comparison with a reference concentration. Here, the obvious choice of the boundary concentration was made, which leads to negative SDI values or seston accumulation due to local primary production in poorly flushed areas. A more 'natural' or logical approach would be to compare seston concentrations with and without aquaculture. However, turning the term for oyster filtration off in Eq. (1) would lead to unrealistically high seston concentrations, as no other seston decay is considered. This would therefore result in a strong overestimation of depletion with the present approach but is well adapted to ecosystem modelling approaches where an exhaustive representation of seston dynamics is considered (Grant et al. 2008). Plew (2011) studied seston depletion by mussel farms with a similar framework also based on tracer transport. His 'inverse' approach where the tracer directly represents seston removed by mussel filtration eliminates the need for a reference seston concentration. However, this method presents 2 major drawbacks, both of which ensue from the 'inverse' approach, i.e. the tracer not representing an actual dissolved or suspended variable. First, as discussed by Plew (2011), the upper limit of seston depletion is not constrained by seston concentration, which could lead to depletions in excess of the available seston or SDI > 100 per cent in the context of the present study. The second caveat relates to the replenishment of removed seston by primary production, which in the 'inverse' method needs to be formulated as a decay of the tracer. By definition, a concentration is constrained to positive values, in other words, a tracer can only decay where it is present. In the seston depletion analogy, this means that primary production is only effective within the plume of depleted waters. Hence, the 'inverse' method would likely lead to an overestimation of both depletion intensity and spatial extent.

Breach effect
In order to evaluate whether the stronger water exchange/renewal of the 1999 topography would translate into increased seston availability, the SDI was computed for the corresponding model set-up and compared to the 2010 estimate. Fig. 8 shows the difference between 1999 and 2010 SDI values. Once again, the effect of the breach is mostly confined to the immediate vicinity of the breach and the BV area. Quite surprisingly, while the 1999 scenario presents the fastest water renewal, it also shows the highest SDI (ΔSDI > 0) corresponding to a deeper depletion in BV and weaker accumulation of seston close to the breach. These results indicate that the balance be - tween oyster filtration and seston supply is such in the BV area that cultured oysters strongly rely on the autochthonous seston production. It also represents a contrasting situation with other related studies showing that an increase in water exchange could improve the shellfish production in certain coastal systems (R. Filgueira et al. unpublished). The net effect of morphological changes on seston availability and ensuing bivalve production depends on the relative levels of primary production, water renewal rates and shellfish filtration pressure. The interaction between these factors ultimately determines whether an embayment relies on locally produced on imported seston.
Using the same parameters of primary production, seston concentration and cultured oyster density, Dame's index method would also predict that BV oysters depend more on local seston production as PPT/CT ∞ 3 and RT/CT ∞ 5. However, it would not predict any changes between the 1999 and 2010 situations, as the tidal prism method does not account for the altered renewal time following the change in topography.
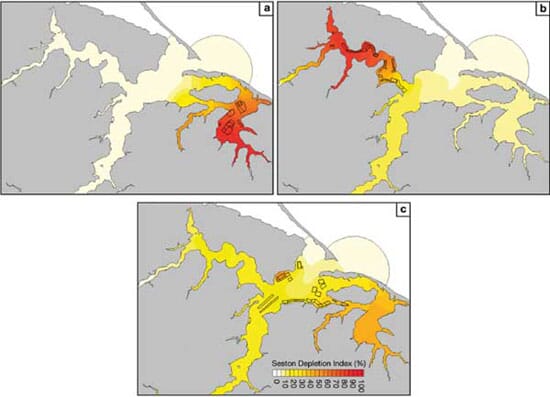
Farm interactions
A concern raised by BV oyster growers during the course of this project relates to the recent development of farms in the CH area and whether these new farms would affect the production capacity of BV operations. The interactions between farming areas within a coastal system definitely represent an issue that will spread with the further development of aquaculture in many regions. Moreover, it constitutes a fundamental question in the context of bayscale management plans. In order to better illustrate the superimposition of water transport and bivalve clearance effects, primary production was removed from the model set-up (α = 0 in Eq. 1). This version of the model was then run for 3 distinct scenarios, each considering active farms in a given region of the studied area (NA, CH or BV). Among the 3 regions, BV farm depletion is the least dispersed within the estuary (Fig. 9a), which is consistent with BV having a rather slow renewal and relying on local seston production. The NA area also shows deep depletions (Fig. 9b), revealing a strong level of aquaculture development relative to its flushing ability, especially in the more upstream reaches. Moreover, the depletion effect diffuses over a wider portion of the estuary, indicating a strong connection between the NA and the rest of the system. Finally, farms in the central and 'upstream' CH region lead to the lowest and most diffuse depletion effects (Fig. 9c). Interestingly, the most noticeable impact of these farms does not occur in CH but rather in BV. Such a result validates the hypothesis made earlier (see 'Dynamics of or - ganic seston') that a significant fraction of the water renewing BV may already have been filtered by oysters cultured in CH. It also explains the strong dependency on locally produced seston of the oysters grown in BV.
Conclusion
A numerical modelling method incorporating the minimal features required to represent the dynamics of organic seston was applied to an existing coastal system with various management issues. The Richi - bucto Estuary may be divided into 3 main areas (BV, CH, and NA) based on water renewal time as well as seston availability. BV showed the strongest sensitivity to seston limitation, resulting from its location within the estuary that accounts for a rather slow water renewal and a significant fraction of the renewing water being pre-filtered by oysters grown in other areas of the system. Moreover, BV was also the most sensitive to observed changes in the sand barrier topo graphy. Surprisingly, the improved water exchange related to such a topographical alteration would be detrimental to the seston availability in BV, as this region mostly depends on locally-produced seston to sustain the cultured shellfish feeding.
The method implemented in our study integrates a very limited set of biological processes and does not account for any feedbacks of shellfish on the ecosystem. As such, the information produced cannot be used to advise on bivalve food limitation or pro - duction capacity. Nonetheless, it may be suitable to address various shellfish aquaculture management issues ranging from site selection, susceptibility to seston limitation, to producing relevant information to address farm interaction issues like competition for food or propagation of diseases or aquatic invasive species. In Richibucto, where a moratorium prohibits new aquaculture development, results were presented to local managers and oyster growers with a clear statement on possible interpretations. The conclusions drawn from the modelling exercise were valuable to a dialogue meant to reassess the moratorium, namely by raising the awareness of the stakeholders to the sensitivity of certain areas of the estuary, especially BV. The SDI was perceived as basic and valuable information for the management of coastal systems with existing shellfish farms. Moreover, the SDI approach was included in a spatial planning exercise in another embayment of the region where the addition of new mussel farms is presently being considered (Malpeque Bay Aquaculture Development Plan, Department of Fisheries and Oceans Canada).
Another characteristic of the modelling method is its flexibility to address upcoming issues like topographical alterations or production of new species. These events are expected as consequences of climate change and increasing seafood demand (Forbes et al. 2004, Bostock et al. 2010).
We acknowledge that, even when kept to a minimal level of complexity, a numerical modelling tool might not be suitable for non-expert users. However, aquaculture management entities often raise complex issues impossible to address using rudimentary tools. We agree that better management practices may only be achieved through a more integrated consultation process between scientific advisors and other stakeholders (Byron et al. 2011, Hopkins & Bailly 2013). The use of simple numerical tools may help this process by providing relevant information in a time frame compatible with a management agenda.
December 2013


